CT中需要多少投影？
CT中的投影数量
CT 体积中的图像质量取决于投影的数量 m。我们到底需要多少个投影才能避免欠采样，避免产生星形伪影和噪声？越多越好？
通常会应用一个规则，根据扫描过程中样品的 X 射线阴影扫过的像素数量 N 来确定 m。为什么会这样？这真的是必要的吗？
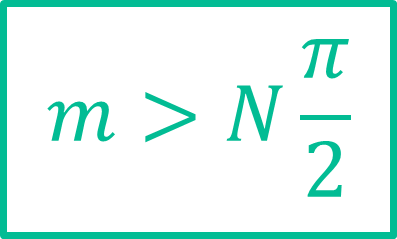
投影数规则的简化推导
这个规则可以通过著名的奈奎斯特定理推导出来。我们使用一个简单的几何考虑来可视化背景。
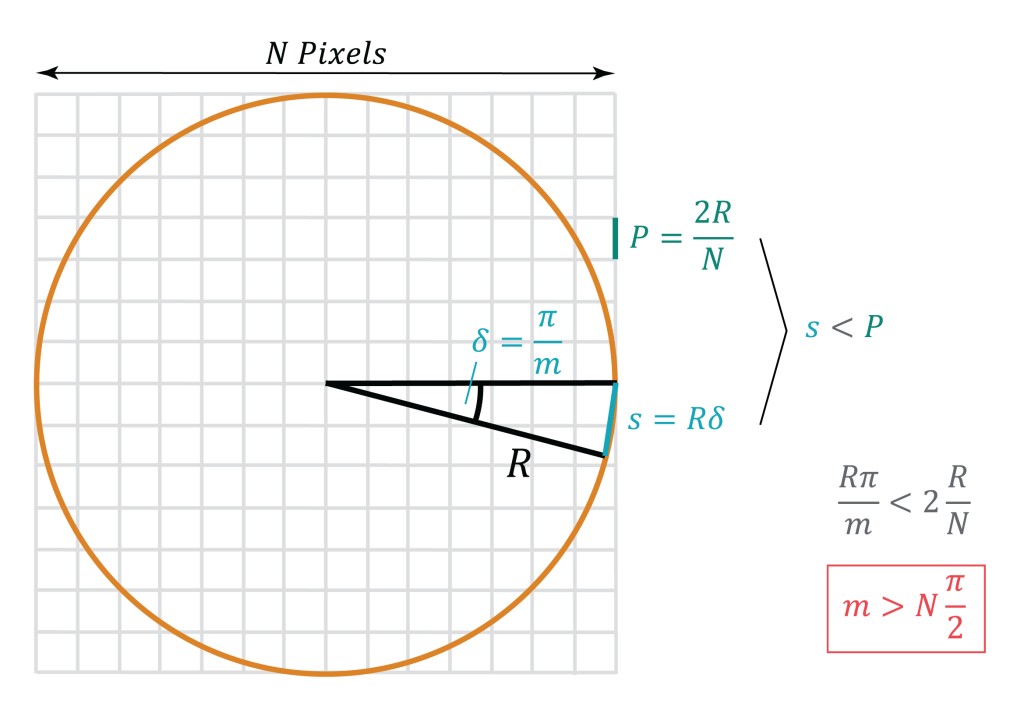
假设扫描过程中 X 射线的阴影扫过 N 个像素，且该阴影被内切于半径 R 的圆内，那么重建的切片大小为 N x N 体素，如图所示。可以推测，扫描中的 X 射线阴影特征在每次投影之间的移动不应超过一个像素。小角度 ∂ 是投影之间的旋转角度。
这意味着小弧长 s 应该小于一个像素宽度 P。一些几何和代数推导得出了这个已知的规则。你是否漏掉了一个 2 的系数？记住，X 射线穿过样品并计数两次。
真的需要这么多投影吗？
如果样品覆盖了例如 4000 x 4000 像素的探测器，投影的数量高达 6300。许多用户认为这是不必要的，他们是对的。任何模糊都会使像素变得更大，从而减少有效像素数量。因此，我们可以简单地在公式中插入另一个 N。
导致模糊的因素有很多：探测器的基本空间分辨率、X 射线在锥束 CT 中的倾斜影响，以及由焦点大小引起的几何不清晰。这些因素是已知的，可以在估算 m 时加以考虑。
实际上，这往往更简单：用户认为他们已经看得足够清楚，并不想花更多时间。
使用更多投影的效果类似于更长的曝光时间或每帧更高的 X 射线剂量：对比噪声比（CNR）会提高。投影数量过少会导致较差的 CNR 和星形伪影模式。